3 Overview of common deep learning models for scRNA-seq analysis

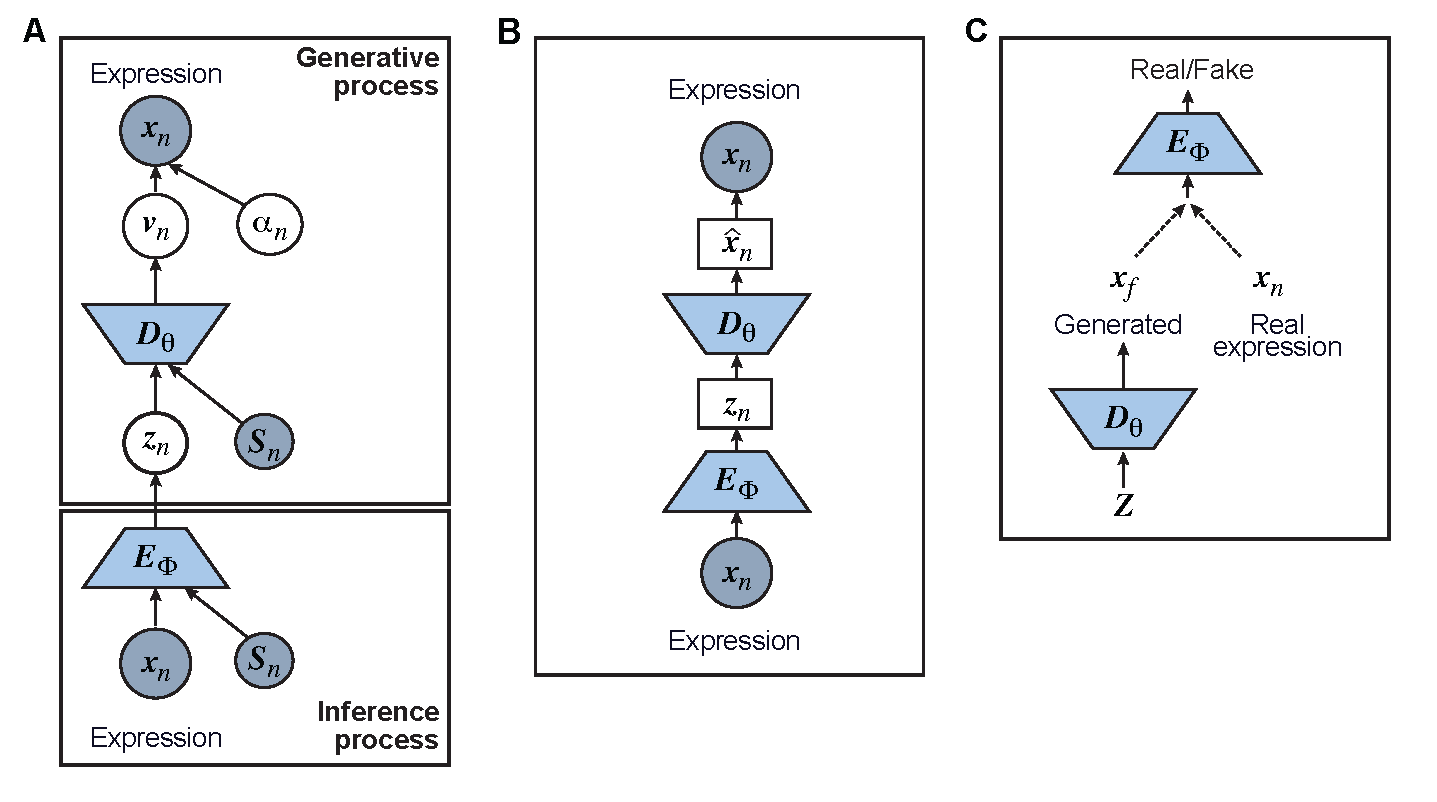
Figure 3.1: Graphical models of the surveyed DL models including A) Variational Autoencoder (VAE); B) Autoencoder (AE); and C) Generative Adversarial Network (GAN)

We start our review by introducing the general formulations of widely used deep learning models. As most of the tasks including batch correction, dimensionality reduction, imputation, and clustering are unsupervised learning tasks, we will give special attention to unsupervised models including variational autoencoder (VAE), the autoencoder (AE), or generative adversarial networks (GAN). We will also discuss the general supervised and transfer learning formulations, which find their applications in cell type predictions and functional studies. We will discuss these models in the context of scRNA-seq, detailing the different features and training strategies of each model and bringing attention to their uniqueness.

3.1 Variational Autoencoder

Let \(x_{n}\) represent a \(G \times 1\) vector of gene expression (UMI counts or normalized, log-transformed expression) of \(G\) genes in cell n, where \(x_{gn}\) denotes gene \(g\)’s expression, which is assumed to follow some distribution \(p(x_{gn} \vert v_{gn}, \alpha_{gn} )\) (e.g., zero-inflated negative binomial (ZINB) or Gaussian), where \(v_{gn}\) and \(\alpha_{gn}\) are parameters of the distribution (e.g., mean, variance, or dispersion) (Fig.3.1A). We consider the first parameter \(v_{gn}\) to be of particular interest (e.g., the mean counts) for the scRNA-seq analysis and is thus further modeled as a function of a d-dimension latent variable \(z_{n} \in R^{d}\) and an observed variable \(s_{n}\) (e.g., the batch ID) by a decoder neural network \(D_{\theta}\) (Fig.3.1A) as

\[\begin{equation} v_{n} = D_{\theta}(z_{n}, s_{n}) \tag{3.1} \end{equation}\]

where the \(g\)th element of \(v_{n}\) is \(v_{gn}\) and \(\theta\) is a vector of decoder weights, \(z_{n} \in \mathbb{R}^{d}\) represents a latent representation of gene expression and is used for visualization and clustering and \(s_{n}\) is an observed variable (e.g., the batch ID). For VAE, \(z_{n}\) is commonly assumed to follow a multivariate standard normal prior, i.e., \(p(z_{n})=N(0,I_{d})\) with \(I_{d}\) being a \(d \times d\) identity matrix. Further,\(\alpha_{gn}\) of \(p(x_{gn} \vert v_{gn}, \alpha_{gn})\) is a nuisance parameter, which has a prior distribution \(p(\alpha_{gn})\) and can be either estimated or marginalized in variational inference. Now define \(\Theta=\{\theta, \alpha_{ng}\forall{n},g\}\) as the collection of the unknown model parameters. Then, \(p(x_{gn} \vert v_{gn}, \alpha_{gn})\) and Eq.(3.1) together define the likelihood \(p(x_{gn} \vert z_{n}, s_{gn}, \Theta)\).

The goal of training or inference is to compute the maximum likelihood estimate of

\[\begin{equation} \hat{\Theta}_{ML} = argmax_{\Theta}\sum_{n=1}^{N}\log(x_{n} \vert s_{n},\Theta) \approx argmax_{\Theta}\sum_{n=1}^{N}\textit{L}(\Theta) \tag{3.2} \end{equation}\]

where \(\textit{L}(\Theta)\) is the evidence lower bound (ELBO),

\[\begin{equation} \textit{L}(\Theta) = E_{q(z_{n} \vert x_{n},s_{n}, \Theta)}[\log{p(x_{n}\vert z_{n},s_{n}, \Theta)}] - D_{KL}[q(z_{n}\vert x_{n},s_{n},\Theta)\|p(z_{n})] \tag{3.3} \end{equation}\]

and \(q(z_{n}│x_{n},s_{n})\) is an approximate to \(p(z_{n}│x_{n},s_{n})\) and assumed as

\[\begin{equation} q(z_{n} \vert x_{n},s_{n})= N(\mu_{z_{n}},diag({\sigma_{Z_{n}}}^2)) \tag{3.4} \end{equation}\]

with \({\mu_{z_{n}},{\sigma_{Z_{n}}}^2}\) given by an encoder network \(E_{\phi}\) (Fig.3.1A) as

\[\begin{equation} {\mu_{z_{n}},{\sigma_{Z_{n}}}^2} = E_{\phi}(x_{n},s_{n}) \tag{3.5} \end{equation}\]

where is weights vector. Now, \(\theta=\{ \theta,\phi, \alpha_{ng}, \forall{n}, g \}\) and Eq.(3.2) is solved by the stochastic gradient descent approach while a model is trained.

All the surveyed papers that deploy VAE follow this general modeling process. However, a more general formulation has a loss function defined as

\[\begin{equation} L(\Theta) = - L(\Theta) + \sum_{k=1}^{K}\lambda_{k}L_{k}(\Theta)\tag{3.6} \end{equation}\]

where \(L_{k}\forall{k}=1,…,K\) are losses for different functions (clustering, cell type prediction, etc) and \(\lambda_{k}\)s are the Lagrange multipliers. With this general formulation, for each paper, we examined the specific choices of data distribution \(p(x_{gn} \vert v_{gn},\alpha_{gn})\) that defines \(L(\Theta)\), different \(L_{k}\) designed for specific functions, and how the decoder and encoder were applied to model different aspects of scRNA-seq data.

3.2 Autoencoders (AEs) for scRNA-seq data

AEs have been proposed to learn the low dimensional latent representation of expression \(x_{n}\). The AE includes an encoder \(E_{\phi}\) and a decoder \(D_{\theta}\) (Fig.3.1B) such that

\[\begin{equation} z_{n}=E_{\phi}(x_{n}); \hat{x_{n}} = D_{\theta}(z_{n}) \tag{3.7} \end{equation}\]

where like VAE \(z_{n} \in R^{d}\) is the d-dimension latent variable, \(\Theta = \{\theta,\phi\}\) are encoder and decoder weight parameters, and \(\hat{x_{n}}\) defines the parameters (e.g. mean) of data distribution and thus the likelihood \(p(x_{n} \vert \Theta)\) (Fig.3.1B). Note that the mean of \(p(x_{n}\vert \Theta)\) is often considered as the imputed and denoised expression of \(x_{n}\). For most common AEs, \(p(x_{n}\vert \Theta)\) assumes a Gaussian distribution and \(\hat{x_{n}}\) becomes the mean of the Gaussian and can be directly used as imputed, normalized gene expression. Nevertheless, additional designs can be introduced to attend imputation specifically. \(p(x_{n}\vert \Theta)\) can also be negative binomial (NB) or ZINB as in DCA (Chen, Ning, and Shi 2019) to model the reads count directly with their parameters defined as functions of \(\hat{x_{n}}\). Additional design can be included in the AE model for batch correction, clustering, and other functions.

The training of the AE is generally carried out by stochastic gradient descent algorithms to minimize the loss with the general expression similar to that of VAE in Eq.(3.6)

\[\begin{equation} L(\Theta)=L_{0}(\Theta)+\sum_{k=1}^{K}\lambda_{k}L_{k}(\Theta) \tag{3.8} \end{equation}\]

where \(L_{0}\) is \(-\log{p(x_{n}\vert \Theta)}\), and \(L_{k}s\) are \(K\) additional function-specific losses. When \(p(x_{n} \vert \Theta)\) is the Gaussian, \(L_{0}\) becomes one of the most commonly used mean square error (MSE) loss

\[\begin{equation} L_{0}(\Theta)=\sum_{n=1}^{N}\|x_{n}-\hat{x_{n}}\|_{2}^{2} \tag{3.9} \end{equation}\]

Because different AE models differ in their AE architectures and the loss functions, we will discuss the specific architecture and the loss functions for each reviewed model.

3.3 Generative adversarial networks (GANs) for scRNA-seq data

GANs have been used for imputation, data generation, and augmentation of the scRNA-seq analysis. Without loss of generality, the GAN, when applied to scRNA-seq, is designed to learn how to generate gene expression profiles from \(p_{x}\), the distribution of \(x_{n}\). The vanilla GAN consists of two deep neural networks [48]. The first network is the generator \(G_{\theta}(z_{n},y_{n})\) with parameter \(\theta\), a noise vector \(z_{n}\) from the distribution \(p_{z}\) and a class label \(y\) (e.g. cell type) and is trained to generate \(x_{f}\), a “fake” a gene expression (Fig.3.1C). The second network is the discriminator network \(D_{\phi_{D}}\) with parameters \(\phi_{D}\), trained to distinguish between the “real” sample \(x\) from \(x_{f}\) (Fig.3.1C). Both networks, \(G_{\theta}\) and \(D_{\phi_{D}}\) are trained to outplay each other, resulting in a minimax game, in which \(G_{\theta}\) is forced by \(D_{\phi_{D}}\) to produce better samples, which, when converge, can fool the discriminator \(D_{\phi_{D}}\), thus becoming samples from \(p_{x}\). The vanilla GAN suffers heavily from training instability and mode collapsing (Rosenberg and Hirschberg 2007). To that end, Wasserstein GAN (WGAN) was developed with the WGAN loss (Rousseeuw 1987):

\[\begin{equation} L(\Theta)=\max_{\phi_{D}}\sum_{n=1}^{N}D_{\phi_{D}}(x_{n})-\sum{n=1}^{N}D_{\phi_{D}}(G_{\theta}(z_{n},y_{n})) \tag{3.10} \end{equation}\]

Additional terms can also be added to Eq.(3.10) to constrain the functions of the generator. Training based on the WGAN loss in Eq.(3.10) amounts to a min-max optimization, which iterates between the discriminator and generator, where each optimization is achieved by a stochastic gradient descent algorithm through backpropagation. The WGAN requires D to be K-Lipschitz continuous (Rosenberg and Hirschberg 2007), which can be satisfied by adding the gradient penalty to the WGAN loss (Strehland and Ghosh 2002). Once the training is done, the generator \(G_{\phi_{G}}\) can be used to generate gene expression profiles of new cells.

3.4 Supervised deep learning models

Supervised deep learning models, including deep neural networks (DNN), convolutional neural network (CNN), and capsule networks (CapsNet), have been used for cell type identifications(Torroja and Sanchez-Cabo 2019; N. Wang L. 2020; Ge et al. 2021) and functional predictions (Yuan and Bar-Joseph 2019). The general supervised deep learning model \(F\) takes \(x_{n}\) as an input and outputs \(p(y_{n}|x_{n})\), the probability of phenotype label \(y_n\) (e.g. a cell type) as

\[\begin{equation} p(y_n│x_n)=F(x_n), \tag{3.11} \end{equation}\]

where \(F\) can be DNN, CNN, or CapsNet. We omit the discussion of DNN and CNN as they are widely used in different applications and there are many excellent surveys on them [55==>Reference Not Found]. We will focus our discussion on CasNet next.

A CasNet takes an expression \(x_n\) to first form a feature extraction network (consisting of \(L\) parallel single-layer neural networks) followed by a classification capsule network. Each of the \(L\) parallel feature extraction layers generates a primary capsule \(u_l∈\mathbb{R}^{d_p}\) as

\[\begin{equation} u_l=ReLU(W_{P,l},x_{n}) \forall{l}=1,…,L, \tag{3.12} \end{equation}\]

where \(W_{P,l}∈\mathbb{R}^{d_p×G}\) is the weight matrix. Then, the primary capsules are fed into the capsule network to compute \(K\) label capsules \(v_k∈\mathbb{R}^{d_t}\), one for each label, as

\[\begin{equation} v_k=squash(\sum_{l}^{L}c_{kl}W_{kl}u_{l}) \space ∀k=1,…,K, \tag{3.13} \end{equation}\]

where \(squash\) is the squashing function (N. D. Patel, Nguang, and Coghill 2007) to normalize the magnitude of its input vector to be less than one, \(W_{kl}\) is another trainable weight matrix, and \(c_{kl} \space \forall{l}=1,…,L\), are the coupling coefficients that represent the probability distribution of each primary capsule’s impact on the predicted label \(k\). Parameters \(c_{kl}\) are not trained but computed through the dynamic routing process proposed in the original capsule networks (N. Wang L. 2020). The magnitude of each capsule \(v_k\) represents the probability of predicting label \(k\) for input \(x_n\). Once trained, the important primary capsules for each label and then the most significant genes for each important primary capsule can be used to interpret biological functions associated with the prediction.

The training of the supervised models for classification overwhelmingly minimizes the cross-entropy loss by stochastic gradient descent computed by a back-propagation algorithm.